Basic and Pythagorean Identities
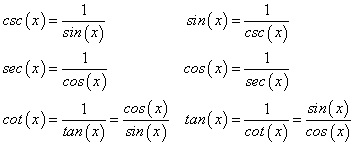Notice how a "co-(something)" trig ratio is always the reciprocal of some "non-co" ratio. You can use this fact to help you keep straight that cosecant goes with sine and secant goes with cosine.
Angle-Sum and -Difference Identities
![tan(2x) = [2 tan(x)] / [1 - tan^2(x)]](http://www.purplemath.com/modules/trig/idents02.gif)
Half-Angle Identities Copyright © Elizabeth Stapel 2010-2011 All Rights Reserved
![sin(x/2) = +/- sqrt[(1 - cos(x))/2], cos(x/2) = +/- sqrt[(1 + cos(x))/2], tan(x/2) = +/- sqrt[(1 - cos(x))/(1 + cos(x))]](http://www.purplemath.com/modules/trig/idents03.gif)
The above identities can be re-stated as:
![tan^2(x) = [1 - cos(2x)] / [1 + cos(2x)]](http://www.purplemath.com/modules/trig/idents04.gif)
Sum Identities
![sin(x)+sin(y)=2sin[(x+y)/2]cos[(x-y)/2], sin(x)-sin(y)=2cos[(x+y)/2]sin[(x-y)/2], cos(x)+cos(y)=2cos[(x+y)/2]cos[(x-y)/2], cos(x)-cos(y)=-2sin[(x+y)/2]sin[(x-y)/2]](http://www.purplemath.com/modules/trig/idents05.gif)
Product Identities
![sin(x)cos(y)=(1/2)[sin(x+y)+sin(x-y)], cos(x)sin(y)=(1/2)[sin(x+y)-sin(x-y)], cos(x)cos(y)=(1/2)[cos(x-y)+cos(x+y)], sin(x)sin(y)=(1/2)[cos(x-y)-cos(x+y)]](http://www.purplemath.com/modules/trig/idents06.gif)
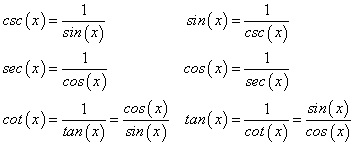
sin2(t) + cos2(t) = 1 tan2(t) + 1 = sec2(t) 1 + cot2(t) = csc2(t)
The above, because they involve squaring and the number 1, are the "Pythagorean" identities. You can see this clearly if you consider the unit circle, where sin(t) = y, cos(t) = x, and the hypotenuse is 1.
sin(–t) = –sin(t) cos(–t) = cos(t) tan(–t) = –tan(t)
Notice in particular that sine and tangent are odd functions, while cosine is an even function.Angle-Sum and -Difference Identities
sin(α + β) = sin(α)cos(β) + cos(α)sin(β)
sin(α – β) = sin(α)cos(β) – cos(α)sin(β)
cos(α + β) = cos(α)cos(β) – sin(α)sin(β)
cos(α – β) = cos(α)cos(β) + sin(α)sin(β)
![tan(a + b) = [tan(a) + tan(b)] / [1 - tan(a)tan(b)], tan(a - b) = [tan(a) - tan(b)] / [1 + tan(a)tan(b)]](http://www.purplemath.com/modules/trig/idents07.gif)
Double-Angle Identitiessin(α – β) = sin(α)cos(β) – cos(α)sin(β)
cos(α + β) = cos(α)cos(β) – sin(α)sin(β)
cos(α – β) = cos(α)cos(β) + sin(α)sin(β)
sin(2x) = 2sin(x)cos(x)
cos(2x) = cos2(x) – sin2(x) = 1 – 2sin2(x) = 2cos2(x) – 1
sin2(x) = ½[1 – cos(2x)]
cos2(x) = ½[1 + cos(2x)]
No comments:
Post a Comment